UVa 00825 – Walking on the Safe Side
Walking in the city of Zhengfang is quite easy because all the roads are like lines on a chessboard, dividing the city into square blocks. Most intersections are safe, and pedestrians can cross directly. However, there are also a few more dangerous intersections, so underground passages or overpasses have been built for pedestrians to cross.
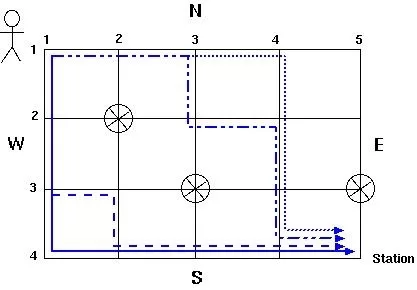
The person wants to travel from the park intersection located in the northwest corner of the city (top-left corner) to the station intersection located in the southeast corner of the city (bottom-right corner). Since he is lazy, he only wants to take the shortest route, which means he will always move down or right, never up or left. Additionally, he dislikes using overpasses or underground passages, so he will avoid these dangerous intersections. Your task is to calculate how many different ways he can walk from the top-left corner to the bottom-right corner.
The following diagram shows 4 east-west roads, 5 north-south roads, and 3 dangerous intersections. Therefore, to walk from the top-left corner to the bottom-right corner, the person needs to traverse (N-1) + (W-1) = 3 + 4 = 7 squares, and there are a total of 4 different ways to do this.
Sample Inputs/Outputs
| Sample Input(s) | Sample Output(s) |
|---|---|
| The first line of input contains a positive integer, indicating how many sets of test data follow.
Each set of test data starts with a line containing 2 integers, W and N (both not exceeding 100), where W represents the number of east-west roads and N represents the number of north-south roads, numbered as shown in the diagram above. The next W lines represent these W east-west roads. Each line starts with the number of the east-west road followed by zero or more distinct integers, representing some dangerous intersections where certain north-south roads intersect with this east-west road. There is a blank line between the first line of input and the first set of test data, as well as between each set of test data. The road depicted in the first Sample Input represents the scenario shown in the diagram above, for reference. | For each set of test data, output a single line containing an integer. This integer represents the number of different ways the person can walk from the top left corner to the bottom right corner. Please leave a blank line between each set of test data. |
| 2 4 5 1 2 2 3 3 5 4 5 5 1 2 1 2 3 4 3 1 2 3 4 1 2 3 5 5 1 2 3 | 4 0 |
Thought Process
In cases where the starting point or the ending point is a dangerous intersection, the answer will be 0.
To access the coordinates of dangerous intersections, it's helpful to convert the coordinates to a 0-based system. This facilitates easier processing when using BFS. You can use getline to extract the coordinates of dangerous intersections as strings and then use a loop to extract the numbers and store them in an array. It's important to note that the test cases may not provide the coordinates in order, so you should use the first number in each line to identify the coordinates.
To implement BFS, you can move either downward or rightward at each step. Declare a 2D array with all elements initialized to 0. While running BFS, if it's possible to move downward or rightward, update the value of the next position in the 2D array by adding the value of the current position in the 2D array. It's important to note that when storing the next BFS starting points, you shouldn't repeat storing the same starting point in the array. You can use a map to check if the current starting point to be stored has already been stored before.
The answer is the value located in the bottom-right corner of the 2D array.
Sample Code-ZeroJudge D198: Walking on the Safe Side
#include <iostream>
#include <vector>
#include <map>
using namespace std;
map<pair<int, int>, int>MAP;
vector<vector<long long int>>step;
int N, M;
pair<int, int> axis (const int a, const int b) {
pair<int, int>tmp;
tmp.first = a;
tmp.second = b;
return tmp;
}
void BFS(vector<pair<int, int>>start) {
if (start.size() == 0) return;
vector<pair<int, int>>newStart;
map<pair<int, int>, int>appear;
for (int i = 0; i<start.size(); i++) {
int y = start[i].first, x = start[i].second;
if (y == N-1 && x == M-1) return;
if (y + 1 < N && MAP[axis(y+1, x)] == 0) {
step[y+1][x] += step[y][x];
if (appear[axis(y+1, x)] == 0) newStart.push_back(axis(y+1, x));
appear[axis(y+1, x)]++;
}
if (x + 1 < M && MAP[axis(y, x+1)] == 0) {
step[y][x+1] += step[y][x];
if (appear[axis(y, x+1)] == 0) newStart.push_back(axis(y, x+1));
appear[axis(y, x+1)]++;
}
}
BFS(newStart);
}
int main() {
cin.sync_with_stdio(0);
cin.tie(0);
int T;
cin >> T;
for (int i = 0; i<T; i++) {
MAP.clear();
step.clear();
cin >> N >> M;
string s;
getline(cin, s);
for (int j = 0; j<N; j++) {
string str, tmp;
vector<int>num;
getline(cin, str);
for (int k = 0; k<str.length(); k++) {
if (str[k] == ' ' && !tmp.empty()) {
num.push_back(stoi(tmp));
tmp = "";
continue;
}
tmp += str[k];
}
if (!tmp.empty()) num.push_back(stoi(tmp));
for (int k = 1; k<num.size(); k++) {
MAP[axis(num[0]-1, num[k]-1)]++;
}
vector<long long int>hi;
for (int k = 0; k<M; k++) hi.push_back(0);
step.push_back(hi);
}
if (MAP[axis(N-1, M-1)] != 0 || MAP[axis(0, 0)] != 0) {
cout << 0 << "\n";
continue;
}
vector<pair<int, int>>start;
start.push_back(axis(0, 0));
step[0][0] = 1;
BFS(start);
cout << step[N-1][M-1] << "\n";
}
}
//ZeroJudge D198
//Dr. SeanXD