ZeroJudge H206: Who's the Strongest?

The destiny of the strong is to battle, and the way to find the strong is like this:

Assuming there are N people, we can divide them into two halves: N/2 people on the left side and N/2 people on the right side. Similarly, for the left half of N/2 people, we can continue to divide them into N/4 people and N/4 people, until it is no longer possible to divide further, i.e., until only 1 person remains.

For intervals with only 1 person, that person is the strongest within the interval. For other intervals, after finding the strongest person on the left side and the strongest person on the right side, it is simply a matter of comparing these two individuals to determine the strongest person within the current interval.

However, the definition of strength often varies; sometimes it's about the small prevailing over the big, and other times it's about the big prevailing over the small. That is, if the current round favors the larger, then the next round will favor the smaller, and the round after that will return to favoring the larger, and so on in succession...

Here, we initially assume the interval of N people favors the larger,
so the intervals divided into N/2, N/2 will favor the smaller, and the subsequently divided N/4, N/4, N/4, N/4 intervals will return to favoring the larger...

Given the value of N and the distinct fighting powers of N individuals from left to right,
according to the comparison method described above, what would be the fighting power of the strongest individual?

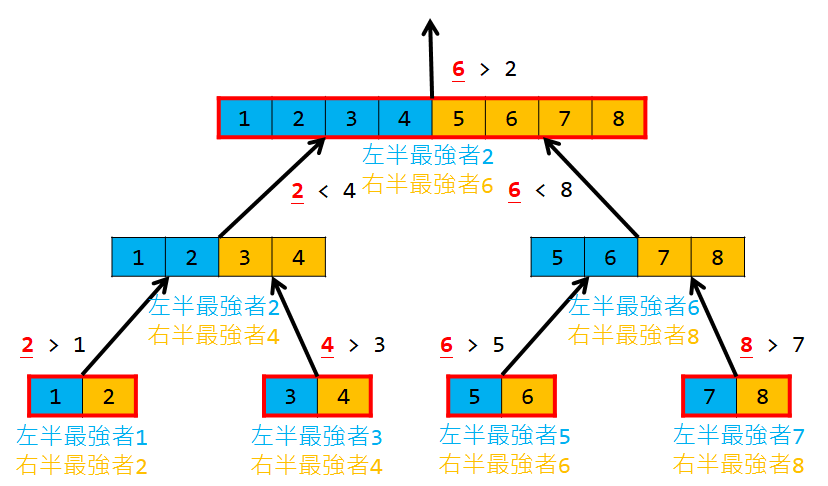
For example, when N = 8 and the fighting powers from left to right are {1, 2, 3, 4, 5, 6, 7, 8}, the strongest individual found will be 6.
Below is the search process, where the red box indicates that the interval is prioritizing the larger fighter, otherwise, it prioritizes the smaller one.

ZeroJudge H206題目舉例圖文說明

Sample Inputs/Outputs

Sample Input(s)Sample Output(s)
The first line contains a positive integer N, which represents the total number of individuals (1 ≤ N ≤ 1024), and N must be a power of 2. The second line consists of N distinct positive integers x_i (1 ≤ x_i ≤ N), separated by spaces from left to right, representing the fighting power of each individual.The fighting power of the strongest individual.
8
1 2 3 4 5 6 7 8		6

Thought Process

Using recursion, the number is continuously divided into halves until there is only one number left in the list (left boundary = right boundary), then returns the current number. The comparison of sizes can be done by flipping a boolean value each time the function is called and returning the maximum or minimum value.

Sample Code－ZeroJudge H206: Who's the Strongest?

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<int>num;

int findMax (int l, int r, bool bigFirst)
{
    if (l == r)
    {
        return num[l];
    }
    if (bigFirst)
    {
        int hi = max(findMax(l, (l+r)/2, false), findMax(((l+r)/2)+1, r, false));
        return hi;
    }
    int hi = min(findMax(l, (l+r)/2, true), findMax(((l+r)/2)+1, r, true));
    return hi;
}

int main() {
    cin.sync_with_stdio(0);
    cin.tie(0);
    int N;
    cin >> N;
    for (int i = 0; i<N; i++)
    {
        int tmp;
        cin >> tmp;
        num.push_back(tmp);
    }
    cout << findMax(0, int(num.size())-1, true) << "\n";
}

//ZeroJudge H206
//Dr. SeanXD
Tags

Related Posts

Comments