ZeroJudge K652: Binary Search Tree Recovery

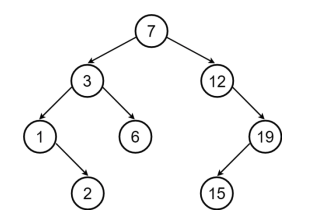
A binary tree is a hierarchical data structure where each node has at most two branches, called the "left subtree" and "right subtree." The branches have a specific left-to-right order and cannot be arbitrarily swapped. A binary search tree (BST), as shown in Figure 1, is either an empty tree (which won't occur in this problem) or a binary tree with the following properties:

  • If the left subtree of any node is not empty, then all nodes in the left subtree have values less than the value of the node.小於它根節點的值
  • If the right subtree of any node is not empty, then all nodes' values in the right subtree are greater than the value of that node.大於它根節點的值
  • The left and right subtrees of any node are also binary search trees.

The information above is referenced from Wikipedia articles on "Binary Tree" and "Binary Search Tree."

A program to output the postorder traversal of a binary search tree refers to:

  1. If the root node has a left subtree, output the postorder traversal result of its left subtree.
  2. If the root node has a right subtree, output the postorder traversal result of its right subtree.
  3. Output the value of the root node.

So the recursive result would be as follows. For example, the postorder traversal of the tree shown below is <P1．．．P8> = .

The task here is to take the given postorder traversal of a binary search tree and reconstruct the tree it represents. Then, explain the output format accordingly.

ZeroJudge K652：二元搜尋數範例

Sample Inputs/Outputs

Sample Input(s)Sample Output(s)
Please output N lines. Each line contains two integers Ui and Fi (1≤i≤N ), representing that the node with value Ui has its parent node Fi. If Ui is the root node, Fi is represented as -1. For all 1 ≤ i < N , Ui <Ui+1.請輸出 N 列，第 i 列有兩個整數 Ui 和 Fi (1 ≤ i ≤ N)，表示值為 Ui 的節點其上
代節點是 F，但如果 i Ui是根節點，上代節點以 -1 表示。其中對於所有的 1 ≤ i < N，
Ui < Ui+1。
8
2 1 6 3 15 19 12 7		1 3
2 1
3 7
6 3
7 -1
12 7
15 19
19 12
7
7 3 1 9 15 20 16		1 9
3 1
7 3
9 15
15 16
16 -1
20 16
1
2		2 -1

Thought Process

This problem can be solved similarly to problem D526 on ZeroJudge. However, instead of building the binary search tree from the leftmost to the rightmost node, here we build it from the rightmost to the leftmost node. When inserting data into the struct, because the data in the binary search tree is not consecutive integers, we can use a map to store the parent node of the current number. When outputting, we can simply use a for loop and iterate through the map using auto it, where it becomes a pair, and then output it.first and it.second. Using endl for output might lead to TLE, so it's better to use cout << "\n" or scanf/printf for faster execution.

Sample Code－ZeroJudge K652: Binary Search Tree Recovery

#include <vector>
#include <map>
#include <stdio.h>
using namespace std;

struct Node {
    int value;
    struct Node *left;
    struct Node *right;
};

int main() {
    int N;
    while (scanf("%d", &N) != EOF)
    {
        map<int, int>MAP;
        vector<int>a;
        for (int i = 0; i<N; i++)
        {
            int tmp;
            scanf("%d", &tmp);
            a.push_back(tmp);
        }
        Node* sean = new Node();
        sean->value = a[a.size()-1];
        Node* root;
        for(int i = N-2; i >= 0; i--) {
            root = sean;
            Node* p = new Node();
            p->value = a[i];
            while(true) {
                if(root->value < a[i]) {
                    if(root->right == nullptr) {
                        MAP[a[i]] = root->value;
                        root->right = p;
                        break;
                    } else {
                        root = root->right;
                    }
                }
                else if(root->value > a[i]) {
                    if(root->left == nullptr) {
                        MAP[a[i]] = root->value;
                        root->left = p;
                        break;
                    } 
                    else {
                        root = root->left;
                    }
                }
            }
        }
        MAP[a[a.size()-1]] = -1;
        for (auto it:MAP)
        {
            printf("%d %d\n", it.first, it.second);
        }
    }
}

//ZeroJudge K652
//Dr. SeanXD
Tags

Related Posts

Comments