ZeroJudge N415: Sculpture

The museum's exhibition hall has N statues, placed at positions 1, 2, ..., N. The weight of the statue placed at position i is known as Wi. The administrator wants to sort them according to their weights: If there are two adjacent statues, namely at positions i and i+1, and Wi > Wi+1, the administrator will use a machine to exchange the positions of the two statues. This action will consume Wi + Wi+1 units of electricity.

The administrator will repeat the aforementioned exchange action until all the statues are sorted in ascending order by weight.

For example, let's consider N = 3 statues with different weights, (W1, W2, W3) = (5, 7, 4). Firstly, exchange the statues at positions 2 and 3, which costs 7 + 4 = 11 units of electricity. At this point, (W1, W2, W3) = (5, 4, 7). Then, exchange the statues at positions 1 and 2, which cost 5 + 4 = 9 units of electricity. Now, (W1, W2, W3) = (4, 5, 7). After sorting, the machine used a total of 11 + 9 = 20 units of electricity.

To assist the administrator, let's calculate how many units of electricity are required to complete the sorting of the statues.

Sample Inputs/Outputs

Thought Process

In this problem, using Bubble Sort to sort and calculate would exceed the time limit. Therefore, Merge Sort should be used. Additionally, the variables in this problem need to be declared as long long int.

收資料的時候宣告一個全域的 Vector<long long int> num，並且將收到的資料存到這個 Vector 中。

使用遞迴的方式來做 Murge Sort，可以將遞迴命名為「murge」，遞迴的回傳值為一個 Vector<long long int>，雖然題目只要計算電力，但是還是需要經過排序的過程所以需要回傳值。

遞迴的參數需要兩個正數 l 和 r，分別代表左右邊界，要將陣列接成一半然後再來排序。首先判斷，if (l >= r)，代表陣列已經被切到只剩下一個資料了，所以宣告一個暫存 Vector<long long int>tmp，並且進行 tmp.push_back(num[l])，代表把這個只剩一個資料的數字存放到這個暫存 Vector 中，並且 return tmp。

如果陣列還有得切的話，就宣告一個整數 m = (l+r)/2，代表目前兩個邊界的中間點。之後要宣告兩個 vector<long long int>，分別是 left 跟 right，代表目前邊界切一半之後的樣子，left = murge(l, m)，right = murge(m+1, r)。這樣子就會再次呼叫遞迴，並且會從只有一個資料的 Vector 開始做計算。

Next, declare an integer lsum to represent the sum of the data in the left array. This will be used in calculating the answer later. You can calculate lsum using a for loop.

先宣告兩個整數 l_index 和 r_index，都是預設為 0，這是我們等一下要取 left 和 right 中資料的順序。再來要跑一個 For迴圈，要跑 left.size() + right.size() 次，因為要將 left 和 right 中的資料排序好並且放到一個新的 Vector<long long int> final 中。主要的思路是判斷 left 和 right 中的資料哪一個比較小就先放到 final 中，可以參考下圖範例：

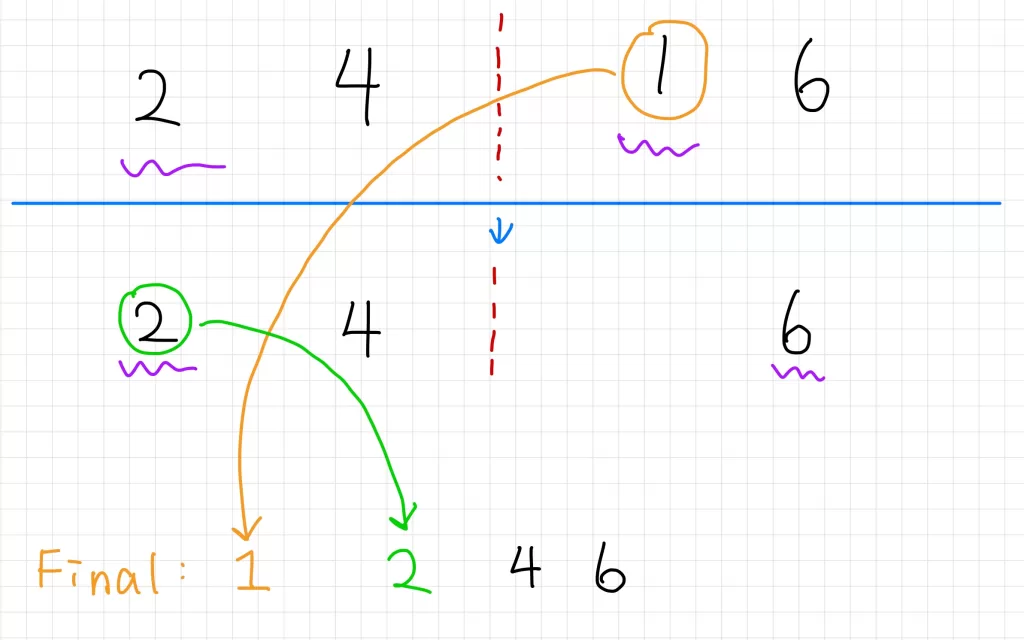
From the example above, we can see that "2" is compared with "3" first. Since "2" is smaller, it is placed into the final vector. Then, "5" is compared with "3", and "3" is placed into the final vector. This process continues until all elements are placed into the final vector.

Before placing elements into the final vector, we need to check if l_index has reached left.size(), indicating that all elements from the left array have been placed into the final vector. Additionally, we need to check if r_index has reached right.size(), indicating that we should not place any more elements from the right array into the final vector. The accurate condition for this check would be: if (l_index == left.size() || (r_index != right.size() && right[r_index] < left[l_index])). If we are taking elements from the left array to place into the final vector, there's no need to compare or sort. However, if we are taking elements from the right array, it indicates that there was an exchange of positions, which requires electricity. The above condition is for placing elements from the right array into the final vector.

如果有進行交換的動作，則需要計算花費了多少電力。首先要判斷這個數字要往左幾格，這個數值其實就是 left.size() – l_index，就是 left 還剩下多少數字的意思。再來要判斷往左走的時候經過了誰，這個就要用到剛剛宣告的「lsum」，因為 lsum 是 left 中的所有數字總和。花費的電力公式就會是：往左幾格*自己＋lsum。最後記得要將 r_index++，這樣下一次的 For迴圈 就會判斷 right 中的下一個資料。

If the data in 'left' is to be stored in 'final', 'lsum' should be decremented by 'left[l_index]', so that when calculating power, it does not double-count the data that has already been put into 'final'. Also, remember to increment 'l_index'.

最後 For迴圈 結束之後要回傳 final。在主程式的地方可以宣告一個 Vector<long long int> tmp = (0, N-1)，之後輸出 ans 即可。

Sample Code－ZeroJudge N415: Sculpture

#include <iostream>
#include <vector>
using namespace std;

vector<long long int>num;
long long int ans = 0;

vector<long long int> murge(const long long int l, const long long int r) {
    if (l >= r) {
        vector<long long int>tmp;
        tmp.push_back(num[l]);
        return tmp;
    }
    const long long int m = (l+r)/2;
    const vector<long long int>left = murge(l, m), right = murge(m+1, r);
    vector<long long int>final;
    long long int lsum = 0, l_index = 0, r_index = 0;
    for (const long long int i : left) lsum += i;
    for (int i = 0; i<left.size()+right.size(); i++) {
        if (l_index == left.size() || (r_index != right.size() && right[r_index] < left[l_index])) {
            ans += (right[r_index]*(left.size()-l_index)) + lsum;
            final.push_back(right[r_index]);
            r_index++;
            continue;
        }
        final.push_back(left[l_index]);
        lsum -= left[l_index];
        l_index++;
    }
    return final;
}

int main() {
    cin.sync_with_stdio(0);
    cin.tie(0);
    long long int N;
    cin >> N;
    for (long long int i = 0; i<N; i++)
    {
        long long int tmp;
        cin >> tmp;
        num.push_back(tmp);
    }
    vector<long long int>v = murge(0, N-1);
    cout << ans << "\n";
}

//ZeroJudge N415
//Dr. SeanXD