"Rectangular bananas" are a new variety of bananas that can only be grown in the intersection area of two rectangles.
For example, here are some situations where rectangular bananas would be produced. When one rectangle is completely covered by another rectangle, it also counts as intersecting (as shown in the lower right diagram):
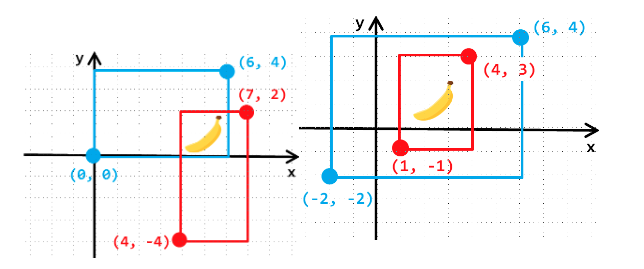
Conversely, here are some situations where rectangular bananas would not be produced. Ｗhen two rectangles only touch edges, it does not count as intersecting (as shown in the lower left diagram):
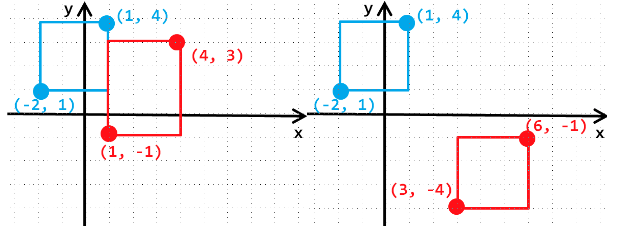
Given two rectangles, please help calculate the area suitable for planting rectangular bananas.
Sample Inputs/Outputs
| Sample Input(s) | Sample Output(s) |
|---|---|
| You can input eight integers (x₁, y₁), (x₂, y₂), (x₃, y₃), (x₄, y₄) where:
(x₁, y₁) represents the bottom-left corner of the first rectangle. (x₂, y₂) represents the top-right corner of the first rectangle. (x₃, y₃) represents the bottom-left corner of the second rectangle. (x₄, y₄) represents the top-right corner of the second rectangle. The coordinates are bounded between -100 and 100 for all xᵢ and yᵢ. | Print the overlapping area of two rectangles; if there is no overlap, print "banana". |
| 0 0 10 10 0 0 5 5 | 25 |
| 0 0 6 4 4 -4 7 2 | 4 |
| 2 2 3 3 3 2 4 3 | banana |
| -2 1 1 4 1 -1 4 3 | banana |
Thought Process
Calculate the left, right, upper, and lower boundaries of the overlapping part, named l (left), r (right), u (upper), and d (down).
l is the maximum of x1 and x3, r is the minimum of x2 and x4, u is the minimum of y2 and y4, and d is the maximum of y1 and y3.
If the four boundaries cannot form a rectangle, it means the two rectangles do not overlap. Specifically, this condition is met when l ≥ r or d ≥ u.
If there is indeed an overlapping area, the area of overlap is calculated as (r−l)×(u−d).
Sample Code－ZeroJudge N687: Rectangular Bananas
#include <iostream>
using namespace std;
int main() {
cin.sync_with_stdio(0);
cin.tie(0);
int x1, x2, x3, x4, y1, y2, y3, y4;
cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3 >> x4 >> y4;
const int l = max(x1, x3), r = min(x2, x4), u = min(y2, y4), d = max(y1, y3);
if (l >= r || d >= u) cout << "banana\n";
else cout << (r-l) * (u-d) << "\n";
}
//ZeroJudge N687
//Dr. SeanXD