ZeroJudge O712: Searching Gems

There is an M × N map, where each cell contains a number representing the number of gems. If the number is -1, it represents a wall.

A robot starts at position (r, c) facing right and follows these movement rules.

  1. If the cell where the robot is located contains 0 gems, the robot's program terminates.
  2. The robot maintains a score, adding the number of gems in the current cell to the score, and then picks up 1 gem from the cell.
  3. If the score is a multiple of k, the robot turns 90 degrees to the right.
  4. If the cell the robot is facing is a wall or out of bounds, it continues to turn 90 degrees to the right until it faces a cell that is neither a wall nor out of bounds, at which point it returns to step 1.
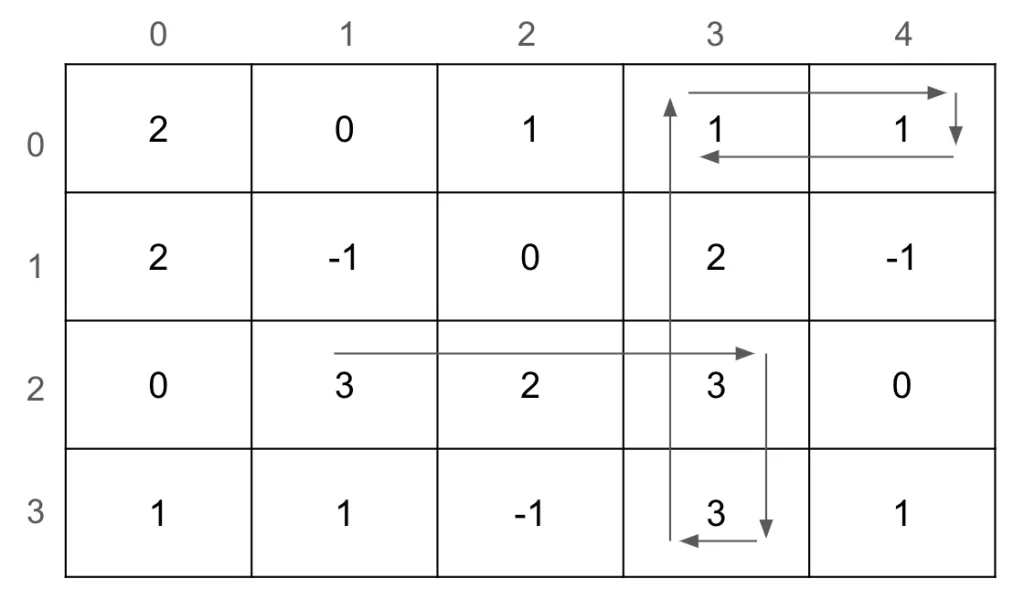
ZeroJudge O712 題目解說

For example, if the robot starts at coordinates (2, 1) and k = 2, it moves right two steps, accumulating a score of 3 + 2 + 3 = 8. Since 8 is a multiple of 2 (k = 2), the robot turns 90 degrees to the right. Next, it moves down one step, increasing the score to 11. It then must turn 90 degrees to the right twice to avoid facing a wall or going out of bounds.

Next, the robot moves one step to coordinates (2, 3). Since it previously picked up one gem, the number of gems at this position is now 2, making the score 13. It then continues moving up two steps to (0, 3), where the score becomes 16. Since 16 is a multiple of 2 (k = 2), the robot turns 90 degrees to the right.

The robot moves forward one step to (0, 4) and then needs to turn 90 degrees to the right twice. It returns to (0, 3), where the number of gems is 0, causing the robot to stop. During this process, the robot picked up a total of 8 gems.

Sample Inputs/Outputs

Sample Input(s)Sample Output(s)
The first line contains five positive integers: M, N, k, r, and c.
1 <= M <= 100
2 <= N <= 100
1 <= k <= 20
0 <= r < M
0 <= c < N
It is guaranteed that the robot's initial position is not a wall. The following M lines each contain N numbers, representing the map's information.		Output the number of gems the robot will collect.
1 7 3 0 4
1 -1 2 1 2 1 0		5
4 5 4 2 1
2 0 1 1 1
2 -1 0 2 -1
0 3 2 3 0
1 1 -1 3 1		8
ZeroJudge O712 Sample Test Cases

Thought Process

Use recursion to move according to the problem's requirements, with the recursion's termination condition being that the current cell has no gems.

Sample Code－ZeroJudge O712: Searching Gems

#include <iostream>
#include <map>
using namespace std;

int M, N, K, R, C, maze[100][100] = {}, score = 0, gem = 0;

map<char, pair<int, int>>loc;

char turnRight(const char dir) {
    if (dir == 'R') return 'D';
    if (dir == 'D') return 'L';
    if (dir == 'L') return 'U';
    return 'R';
}

void walk(const int y, const int x, char dir) {
    if (maze[y][x] == 0) return;
    score += maze[y][x];
    gem++;
    maze[y][x]--;
    if (score % K == 0) {
        dir = turnRight(dir);
    }
    int yy = y + loc[dir].first, xx = x + loc[dir].second;
    while (yy < 0 || yy >= M || xx < 0 || xx >= N || maze[yy][xx] == -1) {
        dir = turnRight(dir);
        yy = y + loc[dir].first, xx = x + loc[dir].second;
    }
    walk(yy, xx, dir);
}

int main() {
    cin.sync_with_stdio(0);
    cin.tie(0);
    loc['R'] = make_pair(0, 1);
    loc['D'] = make_pair(1, 0);
    loc['L'] = make_pair(0, -1);
    loc['U'] = make_pair(-1, 0);
    cin >> M >> N >> K >> R >> C;
    for (int i = 0; i<M; i++) {
        for (int j = 0; j<N; j++) cin >> maze[i][j];
    }
    walk(R, C, 'R');
    cout << gem << "\n";
}

//ZeroJudge O712
//Dr. SeanXD
Tags

Related Posts

Comments