ZeroJudge H084: 牆上海報

有一個由 N 個木板所組成的柵欄，每個木板的高度為 H1, H2, …, HN，有 K 張海報要張貼在柵欄上，每張海報的寬度為 W1, W2, ⋯, WN 並且高度均為 1。

若要張貼海報在高度為 X 的高度，則第 𝑖 張海報需要張貼在一個長度為 Wi 的連續並且高度都不小於 X 的木板上，且每張海報張貼的高度需要一致、按照順序並不能重疊 (可以相連)。詢問最高可以貼到多高的位置。

範例測資

範例輸入範例輸出
第一行有兩個正整數 N 和 K，接下來一行有 
N 個正整數代表每個木板的高度，最後一行有 K 個正整數代表每張海報的寬度。		輸出最大可以張貼的高度。
5 1
6 3 7 5 1
3		3
10 3
5 3 7 5 1 7 5 3 8 4
2 2 1		5

範例測資圖文解說

範例測資 2：

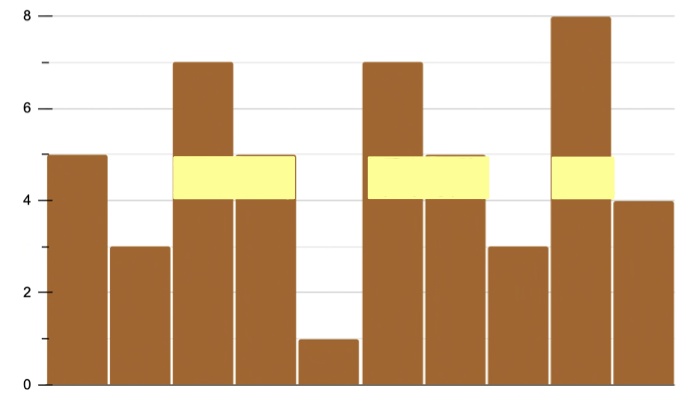
ZeroJudge H084 範例測資圖文解說

柵欄長相如上圖，三張海報 (寬度為 2, 2, 1) 可以貼在高度為 5 的高度。

解題思路

將所有的高度都存放到一個陣列中，裡面不能有重複的高度。進行排序後使用二分搜尋法去取出現在要判斷的高度。

取到現在要判斷的高度後，先從第一塊海報開始判斷，如果有連續且高度 >= 判斷高度的木板，則代表這塊海報放得上去，從下一塊木板開始判斷下一張海報。如果放不上去的話就是從下一塊木板開始判斷目前這張海報。

如果所有海報都能放到目前的高度，就先將目前的高度設定為 ans，並且下一次的二分搜尋往右邊找，反之就往左邊找。當二分搜尋終止時需要再判斷一次最高高度的木板是否可以放得下海報因為二分搜不會跑到最後一個位置。

範例程式碼－ZeroJudge H084: 牆上海報

#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;

int main() {
    cin.sync_with_stdio(0);
    cin.tie(0);
    int N, K;
    vector<int>num, height, poster;
    cin >> N >> K;
    map<int, int>MAP;
    for (int i = 0; i<N; i++)
    {
        int tmp;
        cin >> tmp;
        num.push_back(tmp);
        if (MAP[tmp] == 0) height.push_back(tmp);
        MAP[tmp]++;
    }
    for (int i = 0; i<K; i++)
    {
        int tmp;
        cin >> tmp;
        poster.push_back(tmp);
    }
    sort(height.begin(), height.end());
    int L = 0, R = int(height.size())-1, count = 0, ans = 1;
    while (true)
    {
        if (L >= R) break;
        count = 0;
        int query = height[(L+R)/2];
        for (int i = 0; i<N; i++)
        {
            if (num[i] >= query)
            {
                bool ok = true;
                if (i+poster[count] > N) continue;
                int j = i;
                for (j = i; j<i+poster[count]; j++)
                {
                    if (num[j] < query)
                    {
                        ok = false;
                        i = j;
                        break;
                    }
                }
                if (ok)
                {
                    count++;
                    i = j-1;
                }
            }
        }
        if (count >= K)
        {
            L = ((L+R)/2)+1;
            ans = query;
        }
        else R = ((L+R)/2);
    }
    int query = height[int(height.size())-1];
    count = 0;
    for (int i = 0; i<N; i++)
    {
        if (num[i] >= query)
        {
            bool ok = true;
            if (i+poster[count] > N) continue;
            int j = i;
            for (j = i; j<i+poster[count]; j++)
            {
                if (num[j] < query)
                {
                    ok = false;
                    i = j;
                    break;
                }
            }
            if (ok)
            {
                count++;
                i = j;
            }
        }
    }
    if (count >= K) ans = query;
    cout << ans << "\n";
    
}

//ZeroJudge H084
//Dr. SeanXD
標籤

相關文章

發佈留言