ZeroJudge K652: 二元搜尋樹復原 (BST)

二元樹是一個樹狀結構，樹上每個節點最多有兩個分支，分支被稱為「左子
樹」和「右子樹」。二元樹的分支具有左右次序，不能隨意顛倒。二元搜尋樹（如
圖一）是指是指一顆空樹（本題不會遇到此情況）或是具有下列性質的二元樹：

  • 若任意節點的左子樹不空，則左子樹上所有節點的值均小於它根節點的值
  • 若任意節點的右子樹不空，則右子樹上所有節點的值均大於它根節點的值
  • 任意節點的左、右子樹也分別為二元搜尋樹

以上資料參考自維基百科「二元樹」與「二元搜尋樹」。

一棵二元搜尋樹的後序走訪輸出的程序是指：

  1. 如果根節點存在左子樹，輸出它左子樹後序走訪的結果
  2. 如果根節點存在右子樹，輸出它右子樹後序走訪的結果
  3. 輸出根節點的值

如此遞迴下去。例如：下圖的後序走訪結果為 <P1．．．P8> = <2, 1, 6, 3, 15, 19, 12, 7>。

本題的任務為在給定一棵二元搜尋樹的後序走訪輸出，請找出其代表的二元搜尋樹，並依照輸出格式說明輸出。

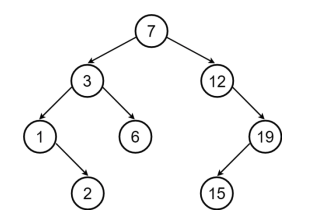
ZeroJudge K652：二元搜尋數範例

範例測資

範例輸入範例輸出
第一列有 1 個正整數 N (1 ≤ N ≤ 2×105)，表示二元搜尋樹有 N 個節點。第二列有 N 個不重複的正整數 P1 ．．． PN (1 ≤ P1 ．．．PN ≤ 109)，彼此皆以一個空白隔開，表示後序走訪輸出的結果。請輸出 N 列，第 i 列有兩個整數 Ui 和 Fi (1 ≤ i ≤ N)，表示值為 Ui 的節點其上
代節點是 F，但如果 i Ui是根節點，上代節點以 -1 表示。其中對於所有的 1 ≤ i < N，
Ui < Ui+1。
8
2 1 6 3 15 19 12 7		1 3
2 1
3 7
6 3
7 -1
12 7
15 19
19 12
7
7 3 1 9 15 20 16		1 9
3 1
7 3
9 15
15 16
16 -1
20 16
1
2		2 -1

解題思路

本題可以參照D526的解題方式，只是從最右邊到最左邊建立二元搜尋樹，當把資料塞到Struct裡時，因為二元搜尋樹的資料不是連續的整數，所以可以使用Map把目前數字的上一個節點存起來。當要輸出時，只需使用For迴圈並使用 (auto it:MAP) 來做輸出，當使用auto it:MAP的時候it會變成一個pair的型態，所以只需輸出 it.first 和 it.second 即可。本題如果使用endl來輸出的時候可能會遇到TLE的情況出現，所以可以使用 cout << “\n” 或是 scanf/printf 來加速。

範例程式碼－ZeroJudge K652: 二元搜尋樹復原 (BST)

#include <vector>
#include <map>
#include <stdio.h>
using namespace std;

struct Node {
    int value;
    struct Node *left;
    struct Node *right;
};

int main() {
    int N;
    while (scanf("%d", &N) != EOF)
    {
        map<int, int>MAP;
        vector<int>a;
        for (int i = 0; i<N; i++)
        {
            int tmp;
            scanf("%d", &tmp);
            a.push_back(tmp);
        }
        Node* sean = new Node();
        sean->value = a[a.size()-1];
        Node* root;
        for(int i = N-2; i >= 0; i--) {
            root = sean;
            Node* p = new Node();
            p->value = a[i];
            while(true) {
                if(root->value < a[i]) {
                    if(root->right == nullptr) {
                        MAP[a[i]] = root->value;
                        root->right = p;
                        break;
                    } else {
                        root = root->right;
                    }
                }
                else if(root->value > a[i]) {
                    if(root->left == nullptr) {
                        MAP[a[i]] = root->value;
                        root->left = p;
                        break;
                    } 
                    else {
                        root = root->left;
                    }
                }
            }
        }
        MAP[a[a.size()-1]] = -1;
        for (auto it:MAP)
        {
            printf("%d %d\n", it.first, it.second);
        }
    }
}

//ZeroJudge K652
//Dr. SeanXD
標籤

相關文章

發佈留言