「矩形香蕉」是一種新品種的香蕉,只能夠種植在兩個矩形重疊也就是相交的區域。
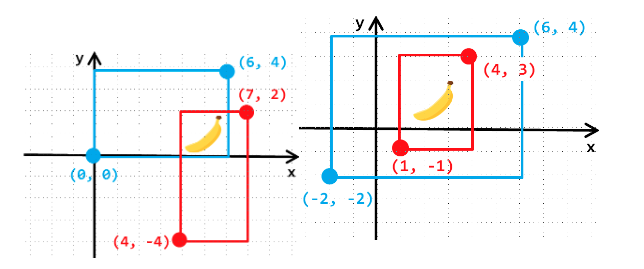
舉例來說,以下是其中幾種會產生矩形香蕉的狀況;比較特別的是當某一矩形完全被另一個矩形覆蓋時,也算是相交(如右下圖):
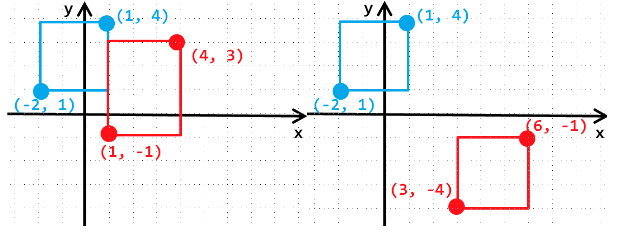
相反地,以下是其中幾種不會產生矩形香蕉的狀況;比較特別的是,當兩個矩形僅是擦邊時,也不算是相交(如左下圖):
給定兩個矩形,請協助計算適合種植矩形香蕉的面積有多大。
範例測資
| 範例輸入 | 範例輸出 |
|---|---|
| 輸入八個整數 (x1, y1), (x2, y2), (x3, y3), (x4, y4) 分別代表: 第一個矩形左下角點 (x1, y1) 和右上角點 (x2, y2) 第二個矩形左下角點 (x3, y3) 和右上角點 (x4, y4) -100 ≤ 對於所有 xi 和 yi ≤ 100 | 印出兩矩形重疊面積,若無重疊則印出 「banana」。 |
| 0 0 10 10 0 0 5 5 | 25 |
| 0 0 6 4 4 -4 7 2 | 4 |
| 2 2 3 3 3 2 4 3 | banana |
| -2 1 1 4 1 -1 4 3 | banana |
解題思路
計算重疊部分的左右、上下邊界,分別命名為 l、r、u、d。
l 就是 x1 和 x3 的最大值,r 是 x2 和 x4 的最小值,u 是 y2 和 y4 的最小值,d 是 y1 和 y3 的最大值。
如果四個邊界無法成為一個矩形的話代表兩個矩形並沒有重疊,也就是當 l >= r 或 d >= u。
如果確實有重疊的部分,重疊的面積為 (r-l) * (u-d)。
範例程式碼-ZeroJudge N687: 矩形香蕉
#include <iostream>
using namespace std;
int main() {
cin.sync_with_stdio(0);
cin.tie(0);
int x1, x2, x3, x4, y1, y2, y3, y4;
cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3 >> x4 >> y4;
const int l = max(x1, x3), r = min(x2, x4), u = min(y2, y4), d = max(y1, y3);
if (l >= r || d >= u) cout << "banana\n";
else cout << (r-l) * (u-d) << "\n";
}
//ZeroJudge N687
//Dr. SeanXD